向量a乘以向量b=(向量a得模长)乘以(向量b的模长)乘以cosα[α为2个向量的夹角];向量a(x1,y1)向量b(x2,y2),向量a乘以向量b=(x1*x2,y1*y2)。

1A向量乘B向量等于什么
点乘
向量A=(x1,y1)
向量B=(x2,y2)
向量A·向量B=|向量A||向量B|cosu=x1x2+y1y2=数值
u为向量A、向量B之间夹角。
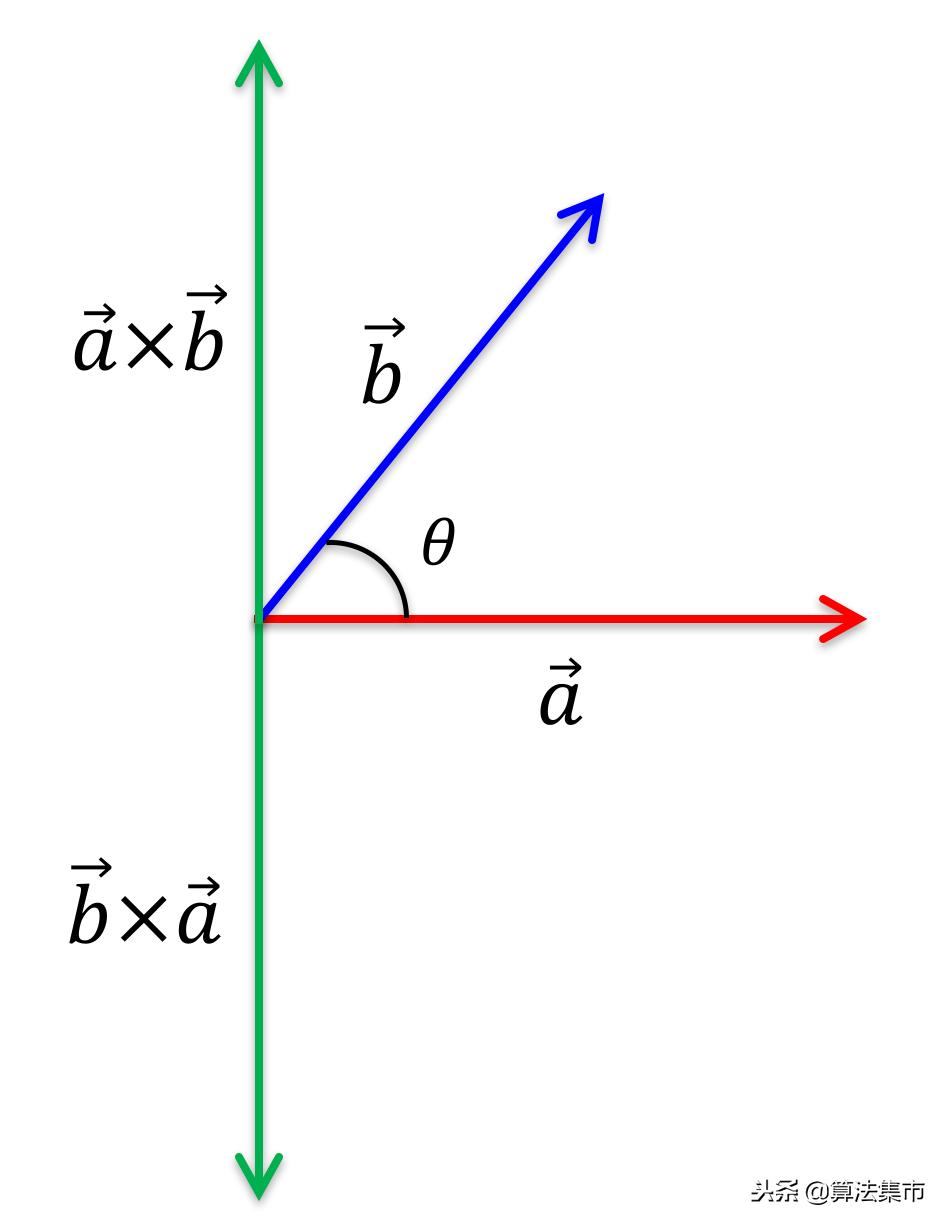
叉乘
向量A×向量B=(x1y2i,x2y2j)=向量
2向量相乘可以分内积和外积
内积就是:ab=丨a丨丨b丨cosα(注意:内积没有方向,叫做点乘)
外积就是:a×b=丨a丨丨b丨sinα(注意:外积是有方向的。)
向量a乘以向量b等于a向量的模乘以b向量的模乘以两个向量夹角的余弦值。
电磁学中,右手定则判断的主要是与力无关的方向。如果是和力有关的则全依靠左手定则。即,关于力的用左手,其他的(一般用于判断感应电流方向)用右手定则。
(这一点常常有人记混,可以发现“力”字向左撇,就用左手;而“电”字向右撇,就用右手)记忆口诀:左通力右生电。左手定则与右手定则其实本质上是相同的 ,它们的不同在于规定手指、手心代表的方向不同而已 , 只是高中阶段为了简单引用了右手定则的概念。
大学阶段 ,凡是涉及到两个向量的叉乘一律用右手定则 。
计算过程如下:
设a=(X1,Y1,Z1),b=(X2,Y2,Z2)
a×b=(Y1Z2-Y2Z1,Z1X2-Z2X1,X1Y2-X2Y1)
(1,2,3)×(4,5,6)=(12-15,12-6,5-8)=(-3,6,-3)
向量的叉乘运算法则为|向量c|=|向量a×向量b|=|a
向量的外积不遵守乘法交换率,因为向量a×向量b=-向量b×向量a。
向量积右手定则使用方法如下:右手除姆指外的四指合并,姆指与其他四指垂直,四指由A向量的方向握向B向量的方向,这时姆指的指向就是A,B向量向量积的方向。就是说,AB向量积的方向垂直于AB向量确定的平面。
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛,通常应用于物理学光学和计算机图形学中。
